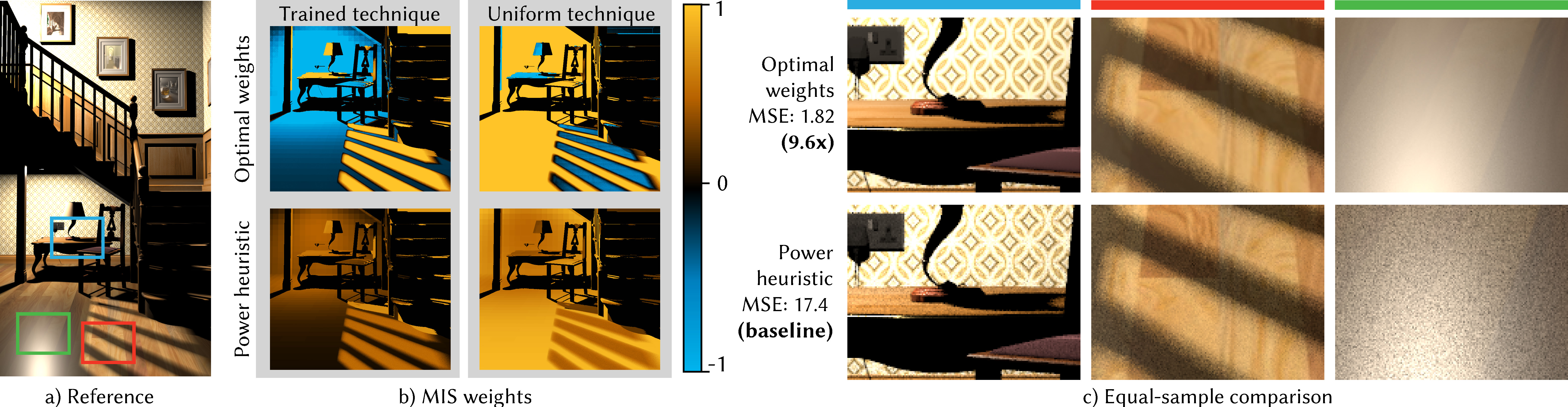
Multiple Importance Sampling (MIS) is a key technique for achieving robustness of Monte Carlo estimators in computer graphics and other fields. We derive optimal weighting functions for MIS that provably minimize the variance of an MIS estimator, given a set of sampling techniques. We show that the resulting variance reduction over the balance heuristic can be higher than predicted by the variance bounds derived by Veach and Guibas, who assumed only non-negative weights in their proof. We theoretically analyze the variance of the optimal MIS weights and show the relation to the variance of the balance heuristic. Furthermore, we establish a connection between the new weighting functions and control variates as previously applied to mixture sampling. We apply the new optimal weights to integration problems in light transport and show that they allow for new design considerations when choosing the appropriate sampling techniques for a given integration problem.