Concept
Our life was hell this semester, but with the semester ending and summer starting we are hoping our lives will have some more color in them.
Spectral Rendering
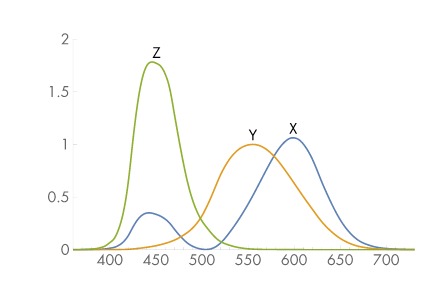
Image Source: Physically Based Rendering, Chapter 5
We wanted to add physical effects of wavelength to our renderer. The effect we were most interested in is the physics of rainbow formation. This process involves diffraction of light to split it into its component wavelengths. To simulate this, we add a wavelength component to our ray. Once the rendering equation is solved for the ray, we project the color sample to the XYZ basis using the wavelength, and then finally get the RGB color from it.

Image Source: Physically Based Rendering, Chapter 5
Rainbow
Aristotelian rainbow in the sky

Before the rainbow theory formulated by Lorenz-Mie, the Greek philosopher Aristotle had a simplified theory for their formulation. This simplified theory which we follow was presented in [1]. It assumes that the sky is a hemispherical dome, and the rainbow is rendered where the angle between the vector to the sun (a pointlight) and the view direction is about about 42 degrees. Additionally a cubic hermite spline interpolation is used to get the wavelength corresponding to the angle. This wavelength is then converted to an RGB color using the process outlined above. The sky is simulated using Perlin noise with five octaves.

Simulating Water Droplet
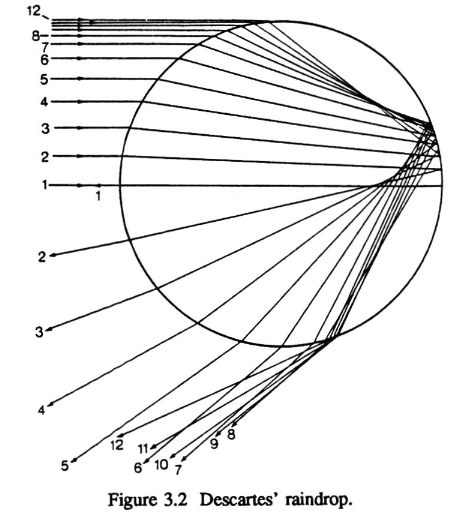
Image Source: [2]
Light is refracted multiple times in a water droplet also causing it to be reflected. The paper we refer to here is [2], which forms an approximate theory of diffraction. The refractive index is modelled as a function of the wavelength. The idea here was that we would be able to see the splitting of the spectrum into its wavelengths. While there are some spectral artefacts visible, the splitting of the spectrum itself is not visible. Our hope was that using volume rendering these artefacts would be more visible as we could further model the diffraction of light along the medium.

Image Source: [2]
Anti-aliasing

We shoot multiple rays per pixel to reduce the aliasing artefacts. On the left is the image with aliasing artefacts visible.

Optimizations
Bounded Volume Hierarchy
We used a Bounded Volume Hierarchy for speeding up intersections of rays with objects. This resulted in a 40x+ speedup in rendering.
Parallelization
The rendering code is parallelized using OpenMP.
Bonus: Volume Rendering

We implemented volume rendering using ray marching. This however does not feature in the final submission due to resource constraints.

References
- Jeppe Revall Frisvad, Niels Jørgen Christensen, and Peter Falster. 2007. The Aristotelian rainbow: from philosophy to computer graphics. In Proceedings of the 5th international conference on Computer graphics and interactive techniques in Australia and Southeast Asia (GRAPHITE ’07). Association for Computing Machinery, New York, NY, USA, 119–128. DOI:https://doi.org/10.1145/1321261.1321282
- F. K. Musgrave. 1989. Prisms and Rainbows: a Dispersion Model for Computer Graphics. In Proceedings of Graphics Interface '89, London, Ontario, Canada. 227-234. DOI:https://doi.org/10.20380/GI1989.30